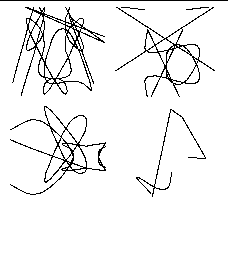Introduction

Interactive fitness evaluation for genetic algorithms was introduced by zoologist Richard Dawkins in his book, "The Blind Watchmaker." The book describes a computer program for evolving images of creatures Dawkins calls "biomorphs" [Daw87]. Each biomorph is produced from a compact genetic code that specifies the creature's particular characteristics. Contained in the code is the essential information necessary to create a bit-mapped image of the creature on the computer screen. Using a technique called interactive evolution, the computer and user collaborate to produce complex and varied insect-like creatures. With interactive evolution, the user selects the most aesthetically pleasing biomorph from a set of creatures displayed on the screen. By randomly mutating the genetic code of the selected biomorph, the computer creates a new generation of biomorphs to display. The new generation is again subjected to the aesthetic selection criteria of the user to produce the following generation. This cycle continues until the user "evolves" a pleasing creature.

Dawkins' idea has spawned several successful applications of interactive evolution to other image design and construction problems ([Sim91], [CJ91], [TL92], [Sth91], [BS93], [Ba93]). This paper presents an interactive evolution system for creating line drawings. The genetic representation and definition of the genetic operators are substantially different from previous interactive evolution systems, and it produces correspondingly unique results. The user interface is similar to other systems (especially Sims' [Sim91] and Dawkins' [Daw87]). An initial population of drawings, either generated randomly by the computer or input by the user, is displayed on the screen. From the displayed set the user selects one drawing for mutation or two drawings for mating. The mating and/or mutation operations are applied to the selected drawings to produce a new set of progeny drawings that supply the input for the next round of user selection. This process is repeated multiple times to "evolve" a drawing of interest to the user. Evolved drawings may be saved and later recalled for mating with other evolved drawings.

Interactive Evolution

Interactive evolution provides a powerful new technique for enabling human-computer collaboration. It is potentially applicable to a wide variety of search problems, provided the candidate solutions can be produced quickly by a computer and evaluated quickly and easily by a human. Since humans are often very good at processing and assessing pictures quickly, interactive evolution is particularly well suited to search problems whose candidate solutions can be represented visually.

Traditionally a genetic algorithm (GA) requires the specification of survival fitness criteria to be evaluated by the computer [Gol89]. This is typically one of the most difficult tasks in designing a GA. With interactive evolution the user performs this step, applying whatever complicated measure of fitness is desired. Unfortunately, including a human evaluator also severely weakens the GA because the human's speed and patience become new limiting factors, restricting the population size and possible number of generations. Despite this drawback, interactive evolution has been used to produce some astounding results that could not have been achieved easily by any other known method [Sim91], [TL92].

The beauty of interactive evolution is that the user need only apply personal fitness criteria, not state or even understand them. This feature of interactive evolution is used very effectively in a system by Caldwell and Johnston for allowing a crime victim to produce a facial composite of a criminal suspect [CJ91]. This system takes advantage of the remarkable human ability to recognize faces. A database of face parts (e.g., eyes, noses, mouths) is used to construct candidate faces, which are then rated by a human operator for their degree of likeness to the suspect. Based on these ratings, the faces are recombined and mutated to produce a new generation of faces. This rating and procreation process is repeated until a likeness to the suspect is achieved. Caldwell and Johnston state that, while "humans have excellent facial recognition ability," they "have great difficulty in recalling facial characteristics with sufficient detail to provide an accurate composite" [CJ91]. This is a perfect example of the ability to apply a complex fitness test without consciously understanding it. Since computers have historically performed poorly at face recognition (compared to humans), the system employs a particularly suitable division of labor between human and computer.

Sims' system uses interactive evolution to create beautiful, abstract color images [Sim91]. The genetic code for an image is a Lisp expression representing a sequence of image-processing functions (i.e., functions that take as input a set of pixel values and associated coordinates, and produce new pixel values as output). Sims uses a fixed set of image-processing primitives, and uses interactive evolution to evolve increasingly complex functions. The search space consists of all Lisp expressions that can be constructed from the primitives. The mutation and mating operators restructure or modify the Lisp expressions and make random parameter changes. Sims also evolves plant forms by applying interactive evolution to L-Systems, grammars that describe biological models of plant growth [Sim91] [LP89].

Other interactive evolution systems of note include: Dawkins', which uses a recursive genetic structure that produces varied, but highly characteristic insect-like forms [Daw87]; Todd and Latham's, which uses constructive solid geometry techniques to evolve "virtual sculptures" [TL92]; Smith's, which uses a Fourier-series-based representation to produce bug-like curved line forms [Sth91]; and Oppenheimer's, which produces life-like 3D tree forms using a recursive fractal representation similar to Dawkins' [Opp89].

These systems use a variety of genetic representations to explore both infinite and large finite spaces. Each system relies on the ability to represent candidate solutions visually and on the human ability to evaluate these solutions quickly and in parallel. The evaluation criteria used are difficult-to-articulate personalized assessments of such poorly defined characteristics as "interesting," "aesthetically beautiful," "good likeness," or "life-like." These are terms whose definitions may vary drastically from person to person or even change from moment to moment in the same person. It is this type of search problem for which interactive evolution provides an exciting new tool.

To date only a handful of interactive evolution applications have been built. These few applications have shown interactive evolution to be an interesting and useful tool, but there is still untapped potential in many other areas as well. One goal of this research is to add to current understanding of interactive evolution by applying it in a new domain. In doing so we hope to gain fresh insight into both its power and its limitations.

At the application level, the goal is to build a new kind of computer-aided drawing tool. Traditional tools use a compact, object-oriented drawing representation that makes it easy for a user to apply many operations to the drawing. Unlike a bit-mapped image, this high-level representation allows the user easy manipulation of individual drawing features, such as the ability to delete or modify individual lines, points, or other objects. However, creation of drawings in this format requires very good eye-hand coordination, and, for anything even slightly complex, a great deal of effort and tedium. Using these tools to create drawings beyond a certain level of complexity can be all but impossible, especially for a non-artist. The work presented here is intended to demonstrate the potential for using interactive evolution to augment and enhance the power of traditional computer-aided drawing tools and to expand the repertoire of the computer-assisted artist.

See Drawing Evolver describes the Drawing Evolver and shows how interactive evolution can be used to create complex drawings in a high-level format. See Discussion discusses our experience using the Drawing Evolver.

Drawing Evolver

The Drawing Evolver is an interactive evolution system written in the C programming language that runs under X Windows on a Unix workstation. Its basic components are: a structured representation for drawings; a means of producing an initial population of drawings; mating and mutation operators; and an operator that produces a drawing from its corresponding genetic code.

Drawing Representation

In the language of biologists, the genetic constitution of an organism is referred to as its genotype, and the physical manifestation of the organism as its phenotype. In the Drawing Evolver, the organisms are drawings whose appearance (or phenotype) is determined by their genetic code (or genotype). The core of the system is the structure of the genotypes used to represent drawings. A genotype consists of an ordered set of "strokes," where each stroke is represented by an ordered set of points and a method for connecting them (e.g., a spline curve or straight lines). A stroke may be loosely thought of as a mark made by a pencil without lifting it off the page. The stroke specification also includes other per-stroke parameters. For example, a symmetry type (horizontal, vertical, both, or neither) is given for each stroke. A set of symmetric marks are encoded as a single mark with a stated symmetry type. In this case several disconnected marks are still referred to as one stroke. The number of strokes in a drawing, as well as the number of points in a stroke, can vary, resulting in genotypes of varying length, and drawings of varying complexity.

In theory, this representation provides for the possibility of any line drawing contained within the drawing frame. The number of possible phenotypes is very large, but finite. Since there are only two possible values (on or off) for every pixel in the drawing frame, and we use a 250 by 250 pixel square frame, there are a total of distinct phenotypes (over 18000 orders of magnitude larger than Caldwell and Johnston's search space of 34 billion possible composites [CJ91]). See : A simple example drawing and its corresponding genotype (below it). Although the drawing has three separate marks, it consists of only two strokes. The jagged stroke has the property of being "horizontally symmetric," so it consists of two separate marks mirroring each other across a vertical axis. illustrates a simple drawing and its corresponding genotype. See : This table describes how to interpret the ASCII text of a drawing genotype. The genotype is a "blueprint" that defines how to construct the drawing. specifies how drawing genotypes are interpreted.

To mutate a drawing, randomly chosen strokes or stroke points are moved, deleted, or added, and stroke parameters are randomly modified. When two drawings are mated, a randomly chosen subset of strokes from each of the parent drawings are combined to form a new drawing. These operations are described in more detail in See Mutation Operator and See Mating Operators.

Operation Modes

The system has two modes of operation that differ with respect to how an initial population of drawings is created. In random mode, the computer creates an initial population of randomly generated drawings. In user-input mode, the user specifies one or more input drawings to use for creating the initial population.

Starting With Randomly Generated Drawings

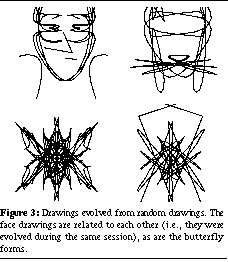
In random mode, the computer initially creates a "screenful" of random drawings (20 in the current version, since that is how many fit comfortably on a 17 inch workstation screen). The user can repeatedly request a new set of drawings until interesting ones are found. Random drawings may also be requested at any time during the evolution process, typically to be used for mating with an evolved drawing. Examples of four initial random drawings are shown in See : Randomly generated drawings. These four drawings were produced automatically, with random choices made for the number of strokes, the stroke points, and stroke parameters. A set of drawings like these may be used as an initial population.. See : Drawings evolved from random drawings. The face drawings are related to each other (i.e., they were evolved during the same session), as are the butterfly forms. shows some drawings that were evolved using random mode. The butterfly forms were created with no preconceived goal in mind and took only a few minutes to produce. The face drawings were created with the specific goal of producing something face-like. This task proved to be much more difficult, taking over an hour to accomplish. However, once a face did emerge, it was quite easy to produce interesting variations on it. This experience motivated the addition of user-input mode described below.

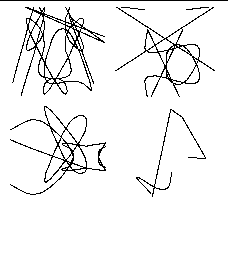
Starting With a User-Input Drawing

In user-input mode, the user provides one or more drawings as a starting point. In this way, the system begins with a coarse solution (or a set of them), and the search is immediately focussed on a potentially rich area. If only one input drawing is given, it and a screenful of its mutated children make up an initial population. If none of the displayed children are sufficiently interesting, the user may reselect the initial drawing for mutation repeatedly to view new sets of mutated children. Since one can produce new sets of children from the same parent(s) repeatedly, the population size at any generation may be as large as the user desires.

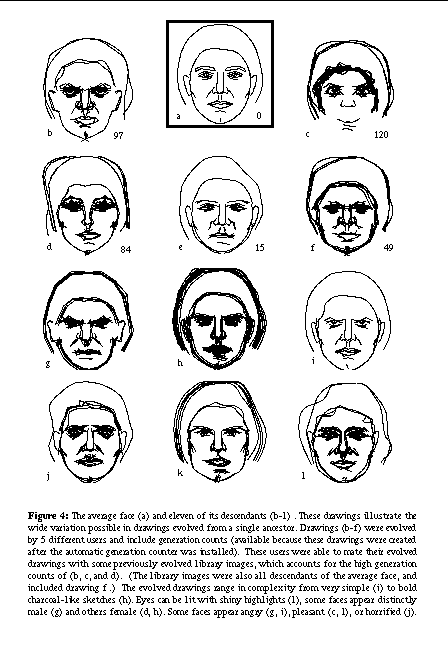
The computed "average face" (from [Bre86]) shown at the top of See : The average face (a) and eleven of its descendants (b-l) . These drawings illustrate the wide variation possible in drawings evolved from a single ancestor. Drawings (b-f) were evolved by 5 different users and include generation counts (available because these drawings were created after the automatic generation counter was installed). These users were able to mate their evolved drawings with some previously evolved library images, which accounts for the high generation counts of (b, c, and d). (The library images were also all descendants of the average face, and included drawing f .) The evolved drawings range in complexity from very simple (i) to bold charcoal-like sketches (h). Eyes can be lit with shiny highlights (l), some faces appear distinctly male (g) and others female (d, h). Some faces appear angry (g, i), pleasant (c, l), or horrified (j). was used in experiments as an initial input drawing and is the sole original ancestor of all drawings presented in the remainder of this paper.1 An average face is a useful initial input drawing because it provides a central point for evolving a variety of different faces. Faces in general are an ideal subject matter for interactive evolution because of the specialized (but poorly understood) human ability to recognize and process them. The decision to limit examples to faces evolved from a single ancestor drawing was made to clarify the point that the variation achieved is a product of the interactive evolution process and not the result of starting from varied drawings. See : The average face (a) and eleven of its descendants (b-l) . These drawings illustrate the wide variation possible in drawings evolved from a single ancestor. Drawings (b-f) were evolved by 5 different users and include generation counts (available because these drawings were created after the automatic generation counter was installed). These users were able to mate their evolved drawings with some previously evolved library images, which accounts for the high generation counts of (b, c, and d). (The library images were also all descendants of the average face, and included drawing f .) The evolved drawings range in complexity from very simple (i) to bold charcoal-like sketches (h). Eyes can be lit with shiny highlights (l), some faces appear distinctly male (g) and others female (d, h). Some faces appear angry (g, i), pleasant (c, l), or horrified (j). shows an assortment of face drawings evolved from the average face and illustrates the wide variation that can be achieved with the system. These drawings were produced from the average face by a simple sequence of mutations and matings. They were typically evolved in fifteen to one hundred generations, usually taking five to thirty minutes to create. Once a library of faces had been evolved, many interesting new faces were produced quickly by combining them. The number of generations required is variable and depends heavily on the user's goals and intentions. Some example generation counts are given in Figure 4. These counts were computed by initializing the average face to a count of zero, increasing the parent's count by one for a mutated child, and increasing the count of the higher valued parent by one for a child produced by mating. Generation counts for drawings mated with library images thus include the number of generations required to create the library images, even though they were already evolved when the user began.

Mutation Operator

A mutated "child" drawing is produced from the genotype of its "parent" by randomly translating, adding, or deleting stroke points or entire strokes, and by randomly modifying stroke parameters (see Table 1). Random translations are effectively a means of jiggling the strokes, much as an artist might do when trying out various small adjustments to the lines in a sketch. Modifying stroke parameters, on the other hand, generally causes more substantial structural changes to the drawing (for example, imagine changing the symmetry property of a stroke from vertical to horizontal). The probability of each type of mutation is individually controlled with adjustable system parameters. By setting the probability of a given mutation type to zero, it is possible to turn off that type of mutation altogether. When evolving drawings in random mode, all mutation types were used; in user-input mode, stroke parameter mutations were turned off. With the average face as an input drawing, it was not useful to change the basic properties of the original face (for example, since one normally always wants two eyes, two ears, etc., it didn't make sense to allow changes to the symmetry properties of the face). By limiting mutations to those that jiggled around existing lines without changing basic properties, it was possible to retain the `face-ness' of the original drawing while still producing a great deal of interesting variation.

The genotype specifies a perturbation factor for each stroke that restricts the distance (in pixels) that the stroke or stroke point may be moved during a single mutation. The genotype also specifies a mutation rate indicating the probability that a given stroke will be mutated during reproduction. In user-input mode the perturbation factors and mutation rates for the input drawing may be tailored to the specific subject matter. For example, the hair outline of the average face was given a larger perturbation factor than the eyes and other small features. If the small features are given too large a perturbation factor, they can jump off the face in one mutation. If the hair outline is given too small a perturbation factor, it's difficult to get any significant variation from the bathing-cap look of the original drawing. The mutation rate for the hair was also set higher than for other parts of the drawing. The perturbation factors and mutation rates can also be mutated, but we have not yet experimented with this capability2.

See : Example of single step mutations starting with the average face. The original average face is shown in (a). This figure is a segment of the screen from an actual run of the system in which the average face was given as an input drawing. Note that small changes in just a few strokes of a drawing can subtly change the appearance of the face. For example, the eyelid mutations in (m) give it a sleepy expression, the point translations in the jaw line of (b) make the jaw more angular and masculine, and the eyebrow mutations in (g) create bushy eyebrows. shows an example set of single step mutations starting with the average face. This is how the initial screen might look when the average face is used as the input drawing. The only active mutation types in this example are stroke deletions and translations, and point additions, deletions, and translations, with translation more likely than other mutation types. See : Mutations from an evolved face (parent left, children a b c). These particular mutations cause subtle differences in facial expression, especially around the eyes. The mutations in (b) create an angrier look than the parent, whereas (a) has a softer friendlier appearance. The eyebrow mutations in (c) create a slightly perplexed look. illustrates the subtle mood and expression changes that the mutation operator can produce in a more complex, evolved face.

Mating Operators

A mating operator takes two parent drawings as input and uses them to produce a child drawing. The basic approach is to choose a subset of the strokes from each parent and combine them to form the child. We experimented with a number of different mating operators, three of which are used in the current system. There are two primary mating schemes (referred to as uniform mating and ID-based mating) and a third hybrid scheme which combines the other two.

Uniform Mating

In uniform mating, each stroke of each parent is independently considered for inclusion in the child. If a fair coin is used to make the inclusion decision, this process will typically produce a child with approximately half of the strokes from each parent. Since this is not necessarily the desired outcome, we randomly choose a weight (or bias) for the coin, with a different weight chosen for each parent. If the weight is chosen to be any value between 0 and 1, the number of strokes in the child might be as many as the sum of the number of strokes in the parents, or as few as one. Hence, a child may look much more or much less complicated than its parents. In practice, we chose to limit the weights to values between .3 and .7, so that the child may differ in complexity from its parents, but not too drastically. Depending on the coin weights chosen, the child may have more in common with one parent than the other. See : Uniform mating (parents above, children below). Note that the children can inherit components of individual features or expression from both parents. In this case, parent (a) has an angry expression and looks more male than female, while parent (b) looks female. Child (c) inherited some of the angry expression from (a), but the darkly outlined eyes and curly lower hairline from (b), making it look more feminine. Assessments of this kind are clearly subjective. illustrates uniform mating.

ID-Based Mating

Uniform mating tends to produce interesting highlighting and shading effects because drawings are combined at a fine level of granularity (e.g., a subset of strokes from one parent's nose are combined with a subset of the strokes from the other parent's nose) and because similar strokes can be overlapped (e.g., the child may receive eyelid strokes from both parents). However, there is no knowledge of individual drawing features (such as the nose or eyes). In contrast, ID-based mating makes it possible to combine the parents at a coarser level, allowing, for example, the child to inherit the mother's nose in its entirety and the father's eyes in their entirety. To accomplish this, an ID field was added to the stroke representation. With the introduction of an ID field, a user can indicate that certain strokes in an input drawing are related (such as those for the eyes) by giving them the same ID. If no IDs are provided, it is assumed that each stroke has a unique ID, which is then assigned automatically. IDs were added to the representation for the average face such that the set of strokes composing each facial feature shared the same ID. To mate two drawings, corresponding sets of strokes (i.e., those with the same ID) from the parents are considered in turn, and one parent is chosen at random to contribute its entire set to the child. If only one parent contains a set of strokes with a particular ID (for example, if the father has ears, but the mother doesn't), a random decision is made as to whether to include that set in the child. See : ID-based mating (parents above, children below). Children receive (for example) the entire set of eye strokes from parent (a) or from parent (b). This is in contrast to uniform mating, where the eyes are more likely to be a mix of the strokes from both parents. Child (d) has inherited the hair, eyebrows, and mouth from parent (a), but the eyes and lack of ears from parent (b), creating an entirely new look. illustrates ID-based mating.

Hybrid Mating

Hybrid mating was developed in an effort to combine the best features of uniform and ID-based mating. For each set of corresponding strokes in the parents, it is decided randomly whether to apply uniform mating or ID-based mating within that set. This mating operator could easily produce a child with the entire set of eye strokes from the mother, the entire set of nose strokes from the father, and some combination of mouth strokes from each.

Discussion

Interactive evolution relies heavily on the user, so each person's experience is different. This section presents some observations on what it feels like to use the Drawing Evolver and an assessment of some of the factors that contribute to its successes and failures.

Since most of the user's time is spent evaluating drawings, it is important to provide a high quality set of candidate solutions at each generation. The set of drawings presented to the user should be sufficiently varied, but must also stay within the user's space-of-interest. These two goals can be in opposition, because allowing more variation among a population of drawings increases the probability that the successful parts of the drawings will be lost as well. Primary factors influencing the quality of candidate solutions are the mutation rates, characteristics of the mating operators, and the genetic representation.

In the Drawing Evolver, a lack of sufficient variation means that the user is sometimes faced with a screenful of drawings whose differences are very subtle, making it difficult to distinguish between them and to make choices. The problem is most evident when using the mutation operator or when mating two very similar parent drawings. To combat this problem with respect to mutation, we use outrageously high mutation rates (e.g., 25%) as compared to the tiny fractional rates used in traditional GAs (or that occur in biological evolution). With respect to mating, having a library of evolved drawings that can be mated with newly evolved drawings was found to be one helpful way to provide the user with a more varied meta-population. Nonetheless, the small viewing sample size and the fact that the viewing sample is composed of children from just one or two parents can still conspire to decrease variation.

The mating operators themselves were also found to have an impact on the variation and quality of drawings. While experimenting with different mating operators, it was somewhat surprising to discover that uniform mating worked well when applied to mutations of the average face. Interesting effects, such as shading and highlighting, began to emerge in the evolved drawings, and the level of intricacy of a drawing increased. If a face acquired two corresponding strokes (e.g., two nose strokes), this often had the effect of producing a sketchy version of the face, with a more three-dimensional and textured look. These are effects that an artist can work very hard to achieve in a drawing, and seeing them emerge in drawings produced by a computer is very exciting. However, because uniform mating embodies no knowledge of the high-level drawing components, it too tends to produce sets of children whose differences are subtle and less dramatic. ID-based mating offers more substantial and dramatic perceptual differences, but is less likely to produce the shading and highlighting effects. Combining both mating types makes it possible to achieve better variation without also losing the interesting effects made possible with uniform mating.

The appropriateness of the representation for the particular search space is yet another factor influencing the quality of the candidate solutions. The representation used in the Drawing Evolver is very general (i.e., it can represent any drawing at all) compared to Caldwell and Johnston's (whose genotype represents faces only) [CJ91]. But to limit our search to faces, the user must filter out the drawings that don't look face-like, while Caldwell and Johnston's users always see only valid faces. Of course, having a larger search space is also an advantage, providing the potential to evolve facial expressions and cartoon or animal faces, as well as many other things. Thus, the choice of representation is likely to involve a trade-off between focussing the search space or narrowing the solution space.

The system is easier and more pleasant to use for browsing than it is for evolving a specified goal image. This is no surprise, since the space contains a myriad of interesting drawings, but a comparatively small number that meet some narrowly specified set of requirements. The narrower the goals, the tougher the search problem. Caldwell and Johnston report success at using their system to evolve a likeness to a criminal suspect, but they use a very tightly constrained search space, and a genotype designed with this specific purpose in mind. The Drawing Evolver, with its larger and less constrained search space, is not particularly good at this task. Attempts to start with the average face and evolve a reasonable likeness to a particular person were not very successful. On the other hand, more loosely specified goals, such as a plan for gender and facial expression were fairly easy to carry out.

Conclusions

The Drawing Evolver allows a user to produce a wide variety of complex sketches with highlighting and shading from a single very simple ancestor drawing. These drawings would be quite difficult and tedious (if not impossible) to produce with most conventional object-oriented computer-aided drawing tools. The user, in a reactive rather than proactive role, is responsible only for selecting among sets of drawings produced by the computer. The user need not have any drawing skill or eye-hand coordination (at least no more than is necessary for selecting drawings with the mouse), but good observational and visual skills are useful to be able to distinguish between sometimes subtly different drawings. The user forfeits absolute control over the outcome, but gains an extended repertoire of possible results.

Interactive evolution is an important new tool for using the computer as a creative collaborator in the exploration of large search spaces. While empowered by human-evaluated fitness testing, it is also limited by the slow pace of interactive use. Despite its limitations, interactive evolution has again proved a powerful tool in a new setting, adding more evidence to suggest that its full potential is yet to be explored.

Acknowledgements

Thanks to Jim Clark, Ted Nesson, Joe Marks, Karl Sims, Steve Smith, and Peter Todd for helpful discussions and encouragement. And special thanks to Karl Sims, whose work inspired this research.

References

[Ba93] E. Baker. Summary: Evolving Line Drawings, Proceedings of the Fifth International Conference on Genetic Algorithms, 1993. Morgan Kaufmann Publishers.

[BS93] E. Baker and M. Seltzer. Evolving Line Drawings. Harvard University Center for Research in Computing Technology, Technical Report-21-93, 1993.

[Bre85] S. Brennan. Caricature Generator: The Dynamic Exaggeration of Faces by Computer. Leonardo, Vol. 18, No.3, pp. 170-178, 1985.

[Bre86] S. Brennan. Cited in Computer Recreations by A. K. Dewdney. Scientific American, Vol. 225, October 1986.

[CJ91] C. Caldwell and V. S. Johnston. Tracking a Criminal Suspect Through Face Space With a Genetic Algorithm. Proceedings of the Fourth International Conference on Genetic Algorithms, pages 416-421, 1991. Morgan Kaufmann Publishers.

[Daw87] R. Dawkins. The Blind Watchmaker. W.W. Norton and Company, New York, London, 1987.

[Gol89] D. E. Goldberg. Genetic Algorithms in Search Optimization and Machine Learning. Addison-Wesley, 1989.

[LP89] A. Lindenmeyer and P. Prusinkiewicz. Developmental Models of Multicellular Organisms: A Computer Graphics Perspective. In Artificial Life, edited by C. G. Langton, Proc. Vol. VI, pages 221-250. Addison-Wesley, 1989.

[Opp89] P. Oppenheimer, The Artificial Menagerie. In Artificial Life, edited by C. G. Langton, Proc. Vol. VI, pages 221-250. Addison-Wesley, 1989.

[Sim91] K. Sims. Artificial Evolution for Computer Graphics. Computer Graphics, 25(4):319-328, July 1991.

[Sth91] J. R. Smith. Designing Biomorphs with an Interactive Genetic Algorithm, Proceedings of the Fourth International Conference on Genetic Algorithms, pages 535-538, 1991. Morgan Kaufmann Publishers.

[[TL92] S. Todd and W. Latham. Evolutionary Art and Computers. Academic Press: Harcourt, Brace, Jovanovich, 1992.